One of the fundamentals of any water-based fire protection system is ensuring that a reliable water supply can adequately meet the demand of the system being served. As design engineers, this boils down to analyzing what water pressure, flow and duration are available to be supplied versus the demand required for a system designed in accordance with NFPA 13, Standard for the Installation of Sprinkler Systems. 

Determination of the available water supply by means of calculation or hydrant flow testing is not the scope of this article. Rather, the focus here is on an approach to confidently estimate water-based fire protection system demand at the early stages of a project, given that detailed hydraulic calculations are generally not undertaken until later stages of design.  

Through this process, system designers and engineers can identify the need for a fire pump or a water storage tank in advance of finalizing system details and building layout.  

Before estimating hydraulic demand for a remote area, it is necessary to identify what exactly is being protected and how it is being protected. Depending on the occupancy, commodity or fire hazard classifications, different amounts of water will be required to control a fire effectively. Also, one must understand the sprinkler systems/sprinklers to be used to protect against the hazard.  

Adjustments may be required to the design area, depending on the type selected (dry system, quick response sprinklers, etc.). Alternatively, the sprinkler may have a minimum required flow that differs from standard spray sprinklers and must be accounted for in determining the required water demand.  

Additionally, designers need to identify what is the most hydraulically remote/demanding area. This may be clear, such as a high hazard area on the highest floor in the building or if the entire building is the same hazard classification. However, if it is unclear, then multiple areas may need to be iteratively analyzed to determine which one is the most demanding. 

Sprinkler System: Estimating Required Water Flow Demand  

To estimate the flow demand, the designer needs to identify the number of fire sprinklers required to be calculated within the design area (i.e., the number of sprinklers anticipated to operate during a fire). NFPA 13 permits multiple approaches (density/area method, room design method, residential sprinkler design or a specific/special application) for determining sprinkler quantity; however, we will use the density/area method here. 

The sprinkler standard now identifies a single value for the minimum required discharge density and hydraulic calculation area based on the hazard classification for the remote area. These values from NFPA 13 are tabulated in Table 1.

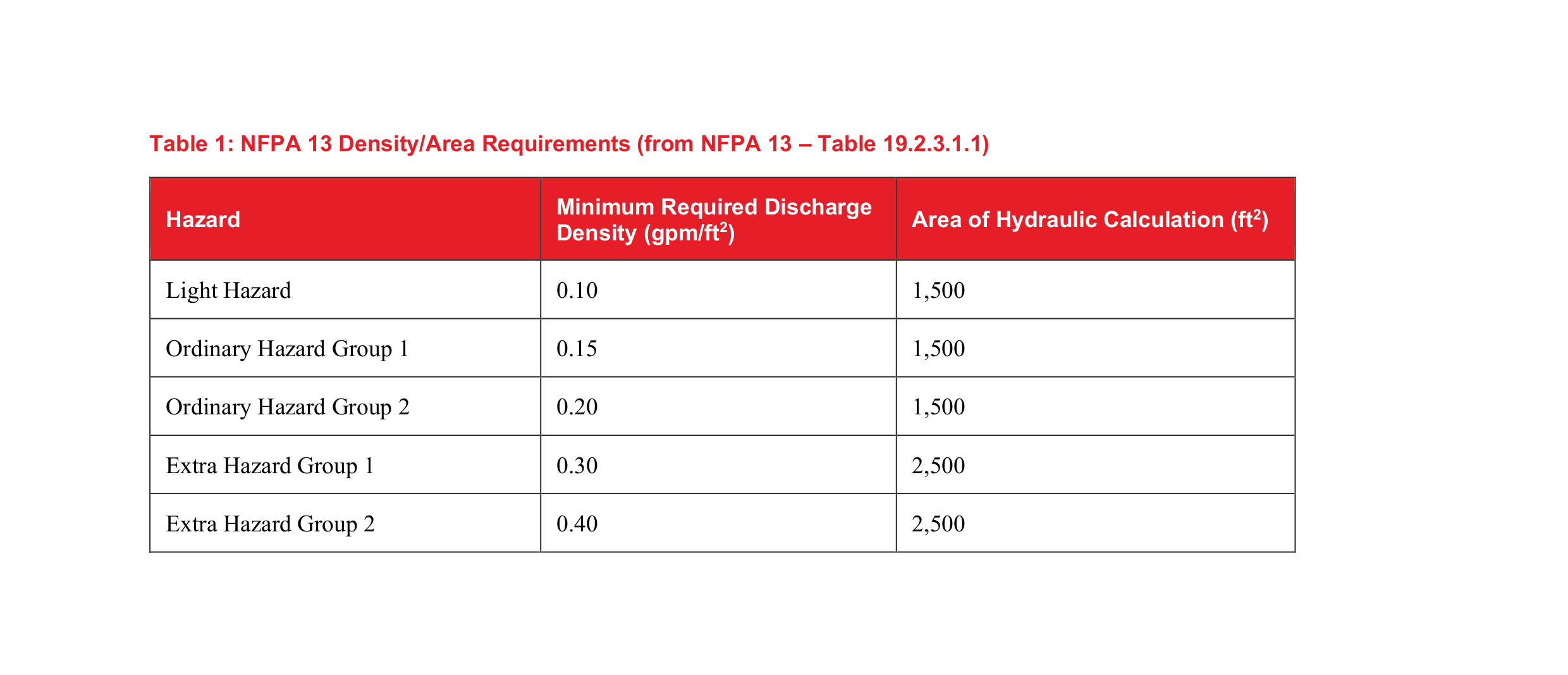
Section 4.3 of NFPA 13 defines each hazard category and gives further guidance on typical occupancies associated with each category within the appendix of the standard. Figures 1 and 2 represent two different hazard categories and help to represent the difference in water demand that is required to protect the spaces 

The quantity of sprinklers required to be calculated within the design area is 

Where:                  

N is the number of sprinklers;

A_HC is the area of hydraulic calculation (ft²) (refer to Table 1);

A_S is the area of coverage per sprinkler (ft²). 

Now that the quantity of sprinklers is understood, the minimum required flow from the most demanding sprinkler must be calculated.

Where: 

Q_DS is the minimum required flow for the most demanding sprinkler (gpm);

Density is the minimum required discharge density (gpm/ft²) (refer to Table 1);

A_S is the area of coverage per sprinkler (ft²). 

After calculating the minimum required flow for the most demanding sprinkler, designers need to check that this flow exceeds the flow calculated using the minimum pressure required by NFPA 13 at the most remote sprinkler (7 psi or as otherwise required by the sprinkler listing). 

Where:         

Q is the flow (gpm);

K is the sprinkler k-factor;

P is the minimum pressure required by NFPA 13 at the most remote sprinkler (psi).

Where the flow from equation 2 (Q_DS) exceeds the flow from equation 3 (Q), the minimum pressure at the most remote sprinkler will satisfy the requirements of NFPA 13. The final step for estimating the water demand is to account for all the sprinklers within the design area.

Where:         

Water demand is the total estimated required water flow demand (gpm);

Q_DS is the minimum required flow for the most demanding sprinkler (gpm);

N is the number of sprinklers;

F_O is the friction loss overage factor; 

Hose demand is the hose stream allowance required by NFPA 13. 

The friction loss overage factor is applied to account for the fact that sprinklers closer to the source will have higher operating pressures, resulting in larger discharge flows. The factor can vary depending on the amount of friction loss expected within the system; however, applying a factor of 30% or more is not unreasonable to conservatively approximate total flow at the early stages of a project. 

Sprinkler System: Estimating Required Pressure 

Having estimated the total required water flow demand, designers need to estimate the pressure required to deliver this water flow demand. To do this, one must calculate the required minimum pressure at the most remote sprinkler.

Where:

P_DS is the required minimum pressure for the most demanding sprinkler (psi);

Q_DS is the previously calculated minimum required flow for the most demanding sprinkler (gpm);

K is the sprinkler k-factor. 

Next, the pressure associated with the change in elevation between the most demanding sprinkler and the water supply must be accounted for.

Where:         

P_E is the pressure created by the elevation difference (psi);

H is the height difference between the most demanding sprinkler and the water supply (ft)

The last portion is estimating the frictional pressure loss from the most demanding sprinkler back to the water supply in which the following can be used to aid in the approximation:

Where:         

P_F is the frictional pressure loss back to the water supply (psi);

L_P is the pipe length back to the water supply (ft);

L_F is the equivalent pipe length associated with fittings (ft);

L_V is the equivalent pipe length associated with valves (ft);

F_F is the average friction loss per foot;

P_V is the frictional pressure loss associated with specialty valves (psi).

For F_F, 0.15 psi/ft is not unreasonable. Refer to the Society of Fire Protection Engineers’ ”SFPE Handbook of Fire Protection Engineering,” Fifth Edition, Chapter 41 Hydraulics.  

For L_F and L_V, refer to NFPA 13, Section 28.2.3 for equivalent lengths. P_V can be approximated based on information from a manufacturer for particular special valves (i.e., backflow preventers). 

The estimated required total system pressure can be summed as follows:

Where:         

P_T is the estimated required total system pressure (psi);

P_DS is the required minimum pressure for the most demanding sprinkler (psi);

P_E is the pressure created by the elevation difference (psi);

P_F is the frictional pressure loss back to the water supply (psi). 

Standpipe System: Estimating Water Flow and Pressure Demand  

As designers, we also need to consider the demand required for the standpipe system (where provided). Unlike sprinkler systems, fire standpipes can be hydraulically calculated relatively early on in the project to a fairly accurate degree. For Class I and Class III systems, hydraulic calculations are necessary to show that the most remote standpipe flows 500 gallons/minute (through its two most remote hose connections). 

The hydraulic calculations must also include 250 gpm of flow per additional standpipe, capped at 1,000 gpm for fully sprinklered buildings and 1,250 gpm for buildings not fully sprinklered. This is true for buildings with floor areas that do not exceed 80,000 square feet/floor, according to Section 7.10.1 of NFPA 14, Standard for the Installation of Standpipe and Hose Systems, 2019 edition. 

In order to be NFPA 14-compliant, a minimum of 100 psi is required at the flowing hose valves.  

If a similar approach as outlined for sprinkler systems is used to estimate the hydraulic demand, then the first step is already done — NFPA 14 has already indicated the demand flow and pressure required at each flow point.  

The remaining step is to estimate pressure losses in the pipe from the most remote hose outlet back to the water supply. Because the standpipe layout is not expected to change drastically as the project progresses, the hydraulic estimate for the standpipe system can be expected to be fairly accurate. That said, designers may opt to apply a safety factor to account for any unexpected changes, as well as additional equivalent length in piping that is added as the design progresses.  

Water Supply Curve 

Now that the required water flow and pressure demand for both the sprinkler and standpipe systems have been estimated, a water supply curve can be plotted to identify if the water supply can adequately meet the demand of the systems. If not, a fire pump or water storage tank may be necessary to meet the system demand and should be accounted for at the early stages of design. 

For additional information and examples of the methods outlined in this article, refer to the SFPE/NFPA “Designer’s Guide to Automatic Sprinkler Systems.”

 A designer cannot undervalue the importance of confidently estimating hydraulic demands early in the project. A 10-psi difference in required pressure or 100 gpm difference in required flow can be the distinction between relying on city water and installing a new fire pump or water storage tank, both of which add cost to a project budget as well as occupy considerable space in the building’s or site’s programming.  

Significant coordination with other trades will be required; if added to the project scope late in the design process, it could be challenging to accommodate. 

 Jack DeVine, EIT, is a fire and life safety consultant in Arup’s Boston office. He has a master’s degree in fire protection engineering from Worcester Polytechnic Institute and has been at Arup for the course of his professional life. He has growing experience in fire sprinkler and fire alarm design as well as code consulting, egress modeling and performance-based fire modeling.  

Robert Accosta Jr., PE, is a licensed fire protection engineer in Arup’s New York office and serves as an alternate member on the NFPA 13 Technical Committee on Sprinkler System Installation Criteria. His expertise focuses on fire protection systems design and life safety code consulting from project inception through beneficial occupancy and closeout. Robert is the past president of SFPE’s New York Metropolitan Chapter.