Most of us have heard about the famous Leaning Tower of Pisa in Italy. Unfortunately for the builders of that tower, the soil under the foundation was not solid ground or bedrock, so the building began to settle. It developed a slight lean during the late stages of its construction because of the massive weight of the stone structure and a small footprint. 

The Tower of Pisa was not intended to lean. However, the 541-foot-tall Montreal Tower, whose 45-degree lean makes it the tallest tilted building in the world — is intentionally inclined. When a building settles and leans and the building systems are not designed to accommodate the settling or leaning, it can be problematic for an owner or developer.  

The freestanding Tower of Pisa was built for ringing the bells to announce the upcoming church services at the adjacent Pisa Cathedral. It was the tallest and heaviest structure built in the city’s Cathedral Square — 186 feet 3 inches tall on the low side and 185 feet 11 inches on the high side, with 8-foot-wide walls at the base and a weight of 16,000 short tons. 

The tower began to lean during construction in the 12th century, and worsened through the completion of construction in the 14th century. By 1990, the tilt had reached 5.5 degrees (https://bbc.in/3qVwsWZ). The structure was stabilized between 1993 and 2001, which reduced the tilt to 3.97 degrees. 

The builders of the Pisa tower were not likely to have had the knowledge or experience with foundation systems design that today’s engineers do, so their work was likely with little knowledge of soil types, bearing capacity of various types of soils or knowledge of the weight of the building versus the soil type and design of different foundation systems.  

Why Does a Building Lean?  

Generally, a lean in a tall building structure is a result of the massive weight of the building pushing down on the ground under the foundation of the building, causing the building to settle into the soil. When the soil is not of an even density, or if the foundation footings are not distributed evenly, the settling can be more on one side or another, causing a building to lean.  

If the ground under the building is not bedrock, or if the pier foundations do not go all the way to bedrock, and the soil under the building is not of a uniform soil density, or if organics are in the soil or fault lines or variations in the soil type from one side of a foundation to the other, this could lead to uneven settling of the building foundation.  

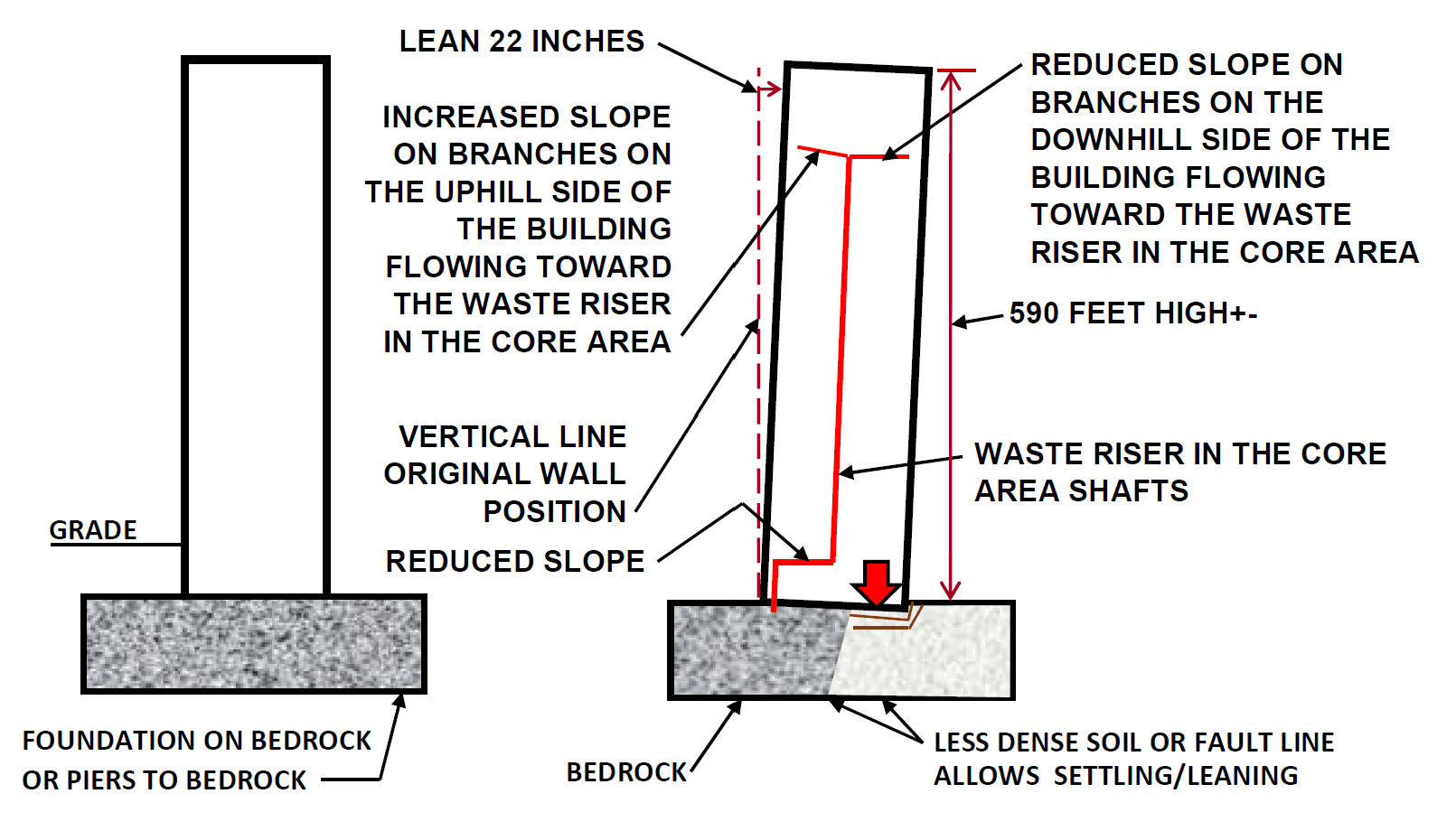
The taller a building is, the heavier it is, with more potential for a settling foundation; the leaning can be more pronounced with a building’s height. When a building leans, the uphill branch increases in slope and the downhill branch flattens or decreases in slope as shown in Figure 1.  

Settling and tilting or leaning of buildings is an age-old issue; many of the older and ancient towers have significant leaning issues. Many of the older, taller, leaning structures are heavy stone towers for the purpose of a lookout, church steeple, bell tower or clock tower. However, they do not have plumbing in these tall towers, so there has not been much issue with leaning buildings in modern times.  

In some cases, the tilt of a building is measured in inches or millimeters of offset from vertical at the top of the building. Another way is to measure the degrees of leaning from vertical. Sometimes the bedrock is so deep, the structural engineers will choose to design a structural mat foundation or a pier foundation with a series of holes drilled deep enough where the friction of the soil against the walls of the pier is enough to resist the weight of the building pushing down from above with some safety factor.  

Since the earthquake in San Francisco, we learned that the soil in many parts of the city turned to liquid. We all became familiar with the term liquefaction as we watched many buildings in the bay area collapse because of the soils there.  

This is something that should be considered when constructing a building in seismic areas or areas with poor soil quality. The bedrock can be very deep, and building a foundation to bedrock can drive up the cost of a foundation that is designed to hold up a heavy building.  

Some famous leaning buildings are listed here: 

Building Name (Country)               Year Built   Degrees of offset from vertical (Height) 

Tiger Hill Pagoda (China)                       960 AD                  3.0      (44 m)

Two Towers of Bologna, short (Italy)        1119 AD                4.0      (47 m)

Two Towers of Bologna, tall (Italy)          1119 AD                1.3      (95m)

Tower of Pisa (Italy)                             1370 AD                3.97     (56 m)

Bad Frankenhausen Church Tower (Ger.)  1382 AD                4.8      (55 m)

Suurhusen Church Tower (Ger.)              1450 AD                5.19     (27 m)

Nevyansk Tower (Russia)                      1732 AD                3.0      (57 m)

Big Ben Clock Tower (London, England)    1858 AD                0.26     (90 m)

Millennium Tower (San Francisco, USA)    2016 AD                0.00316        (176 m, 590 ft)  

Most of the older buildings in this list were bell towers, clock towers, church steeples or watch towers with no indoor plumbing pipe.  

How Does Leaning Affect Plumbing Systems? 

If a building starts to lean and has drains that slope to an interior waste stack, then the sloping drain branches on one side of the stack will see increased slope while the sloping drain branches on the other side of the stack will see decreased slope. Depending on several factors, including the initial slope and other variables, the amount of leaning to cause drainage problems could vary. When a tall building settles and leans, it can cause plumbing drainage problems. 

With modern buildings, leaning just a little amount can affect the flow of waste in sloping drains. Settling drains can create shear stresses and rupture pipe penetrating foundation walls; they also can cause pipe to lose slope or experience reverse slopes.  

The Millennium Tower in San Francisco has had a lot of press about its leaning condition. The reported lean was 22 inches for a 590-foot-tall building, which works out to be 0.0033 degrees of lean for the tower. It is not that significant compared to the Tower of Pisa, but it is reportedly enough to affect the flow of waste in the drains.  

Using mathematical models, we can calculate what would happen to a theoretical drain that is installed at the minimum slope required by code. Then we can subtract the reduction of slope associated with a leaning building and input the information into the Manning Formula to see if it effects the flow velocity in a negative way. 

Using the Manning Formula on a 3-inch or 4-inch branch drain installed at the minimum slope of 1/8 of an inch of fall for each foot of run, it is equal to a slope of 0.0104 percent, or approximately 1 percent slope. If a building is tilted 0.0033 degrees, we would subtract the degrees of tilt from the minimum degrees as installed (or as mandated by code) to get the resulting slope. If we use the code minimum, the resulting slope after deducting for the lean would be 0.0071 percent. 

We could then plug that slope into the Manning Formula, along with the other variables, and determine if the flow velocity would be sufficient. 

The Manning Formula is used to calculate cross-sectional average velocity flow in open channels and drainage pipes: 

v = (kn/n) Rh2/3 S1/2  

Where:

v = cross-sectional mean velocity (ft/s, m/s)

kn = 1.486 for English units and 1.0 for SI units

n = Manning coefficient of roughness; cast iron is approximately 0.012

Rh = hydraulic radius (ft, m)

S = slope or gradient of pipe (ft/ft, m/m) 

In the formula, we would input the following numbers:

 n = 0.012 = cast iron CI or ductile iron DI, new. (Plastic or stainless-steel pipe may have a slightly better n value, but there are many considerations for plastic pipe in high-rise buildings that require firestopping. There are also noise issues with plastic pipe and, to a lesser degree, stainless-steel tubing that meets the standard ASME A112.3.1. Stainless Steel Drainage Systems for Sanitary DWV, Storm, and Vacuum Applications, Above and Below-Ground.) 

Rh = 4-inch CI pipe = 0.33 feet 

S = 1/8 inch/foot minimum = 0.0104 percent (Subtract 0.0031 percent from the minimum slope to input the resulting slope value of 0.0071 percent slope.)  

Hydraulic radius can be expressed as 

Rh = A/Pw  

Where: 

A = cross-sectional area of flow (ft², m)

Pw = wetted perimeter (ft, m) 

The flow quantity in cubic feet per second in a sloping pipe can be solved with this formula: 

Q = A x V 

Where: 

Q = the flow in cubic feet per second, which can be converted to gallons per minute.

A = The cross-sectional area of flow (ft, m) (Sanitary drains are designed to flow no more than half-full to prevent siphoning of traps.)

V = Velocity of flow calculated from the Manning Formula 

To correct for the loss of slope in a tilting building, we would subtract the percent of lean from the original slope of the pipe. Assuming a 0.0104 minimum slope at installation per the plumbing code, minus the lean because of the settling or tilting of a building, it would be 0.0033 percent, resulting in a slope of 0.0071 percent. 

If you plug the slope of 0.0073 percent into the Manning Formula, the resulting velocity will be just under 2 feet/second and would allow solids to fall out of suspension in longer pipe runs. A velocity under 2 feet/second is not adequate for a good scouring action and will promote solids settling to the bottom of the drain.  

Of course, this is just a calculation. I have not examined the building, the actual installed pipe slopes, the pipe materials, the condition and the roughness of the interior of the pipes or the pipe diameters, but the laws of physics and the variables can be determined and updated as slopes change. The performance of the plumbing system will change if the slope changes and this can all be refined and calculated.  

How Does Leaning Affect Drain Line Transport?  

As a building leans, the slope of the drains change. The slope of a drain effects the flow velocity and capacity of a drain and the ability of a drain to transport solid wastes. Sloping drains are calculated using the Manning Formula to determine the velocity of sloping drains; another formula can be used to determine the capacity in gallons per minute based on the drain flowing half-full.  

The minimum velocity in the drain is important to calculate to keep solids in suspension in a flowing drain. If a drain is too flat, then the velocity of the waste water flow can be below 2 feet/second, which will be too low to keep solids suspended and have a scouring action.  

The Manning Formula is used to calculate the velocity in sloping drains and then we convert to volume in gallons per minute for a given pipe size, coefficient of roughness and slope to maintain a minimum velocity. This formula is the basis for the plumbing code sanitary drainage tables for various-sized pipe and minimum slopes, and fixture unit values for sanitary drains to not exceed one-half full flow.  

If a drain flows too full, then air may not move through the top of the drain, creating positive and negative pressures that can blow out or siphon fixture traps.  

If the drains are installed too flat, the velocity will be too low and solids will fall out of suspension and settle on the bottom of the horizontal drains. This creates a condition where drains will block up over time, and on a continuing basis, requiring constant drain cleaning.  

Low-Flow Fixtures Compound the Problem 

When you consider the reduced flows associated with new ultra-low-flow (ULF) fixtures that are mandated in California for water conservation to flush with no more than 1.28 gallons/flush, there will, more likely than not, be some areas where some drain configurations with long horizontal runs will not perform very well as pipe slopes decrease.  

In the past, plumbing fixture standards required water closets to flush solids 40 feet down a branch drain line. Today, with water conservation efforts and ULF fixtures, proper drain line transport and clearing a branch drain with a single flush is extremely difficult. So, the 40-foot drain line transport of all solids in the fixture branch was removed from the fixture standards performance testing with the understanding that subsequent fixture uses will help move solids down the drain.  

When there is no subsequent use or there is a seldom-used fixture or long horizontal runs with only a few plumbing fixtures, drain blockages are more likely to occur. In some of these extreme cases, an engineer may consider installing a solenoid valve in a water supply line to occasionally flush water through an air gap into a hub drain to periodically flush critical horizontal branches and prevent solids from settling in a branch drain and creating an unsanitary condition.  

Fixture usage, length, size and slope of the horizontal branch line and flow required for an adequate flush and water conservation should all be considered by the design engineer.  

Drains should be cleaned with professional drain cleaning machines. Drain cleaning chemicals should never be used to clean out plugged-up drains because chemicals can create a hazard to the workers and building occupants. Also, chemicals can damage drain piping and create very costly repairs to replace horizontal drains and stacks. 

Taller buildings move more at the top than shorter buildings when the foundation settles. For example: Given a building that is 100 feet wide at the base and 100 feet tall, the building would be similar to a cube. If the foundation settles downward on only one side for 1 inch, theoretically, if the height is the same as the width, the top of the building would lean 1 inch in the direction of where the settling occurred. 

Or, given a building that is 100 feet wide at the base and 500 feet tall, the building would have a height-to-width ratio of 5-to-1. If the foundation settles downward on only one side for 1 inch, then the top of the building would lean only 1 inch at the 100-foot elevation. At the 500-foot elevation, the building would move or lean five times as much, but the slope will be the same in both buildings.  

Of course, this is a simple explanation, and the settling can be dynamic, occurring in multiple directions. If settling is uniform, or even, the building could still be vertical, it will just sink. There could be little to no leaning, but the settling creates shear forces and stress at exterior wall penetrations that could shear off utilities or damage seals in the foundation wall, allowing groundwater intrusion around pipe passing through basement walls.  

In part 2, we’ll discuss a case study of soil settling under a building and shear forces acting on piping near foundation walls.